The Common Ownership Trilemma

Introduction

Overlapping ownership of large publicly traded companies in the United States has grown dramatically in recent decades.1 The list of largest shareholders of almost any publicly traded company has a similar set of shareholders, namely the largest asset managers.2 Moreover, the blocks of shares held by these asset managers are by now substantial, and they keep growing. Why has common ownership increased so much, and what are the consequences for antitrust and for the economy more generally?

Recent empirical studies applied theoretical results3 to measure common ownership in the airline and banking industries and showed that the level of concentration from common ownership is, on average, very high, and also that higher common ownership is associated with higher prices.4 This has led to a substantive debate on the implications of common ownership for antitrust practice. Professor Einer Elhauge has argued that anticompetitive horizontal shareholding is banned by Section 7 of the Clayton Act,5 since its language is not limited to full mergers but also covers partial acquisitions of stock.6 Under this reasoning, injured plaintiffs would therefore be able to bring private actions to recover the damages caused by the anticompetitive effects.7 Professor Jonathan Baker has also raised concerns, noting that the rise of common ownership “raises the possibility that a modern-day antitrust loophole or blind spot has . . . been allowing firms to exercise market power across the economy.”8 Professors Eric Posner, Fiona Scott Morton, and Glen Weyl have proposed a policy which would limit the amount of shares that diversified asset managers can hold in competing companies.9

Professors Edward Rock and Daniel Rubinfeld have called for a more restrained approach.10 They have argued that managerial entrenchment and agency costs could limit the extent to which anticompetitive incentives at the shareholder level could actually impact firms’ strategic plans.11 A similar argument was made by Professors Lucian Bebchuk and Scott Hirst.12 Federal Trade Commission (FTC) Commissioner Noah Joshua Phillips has expressed similar views, arguing that agency costs could mitigate anticompetitive effects, to such an extent that in practice concerns about even substantial overlapping ownership of large blocks of stock might be minimized.13 Department of Justice Assistant Attorney General Makan Delrahim has expressed concerns that using antitrust laws against common ownership could harm investors: “If there is an issue with common ownership of competitors by institutional investors, and the Antitrust Division acts to address the effect on competition, we want to ensure any fix doesn’t chill innovation or harm investors.”14

On the other hand, Anna Tzanaki (as well as Rock and Rubinfeld in another paper) has argued that Elhauge’s unilateral effects analysis might underestimate the anticompetitive potential of overlapping ownership, because it ignores the possibility of coordinated effects.15

In this Essay, I attempt to connect this policy debate to some of the ongoing economic debates. I start from the question of why common ownership has increased and argue that the main reason is the rise of portfolio diversification. As diversification has become increasingly cheaper and more accessible to the public, an increasing variety of financial instruments (most prominently index funds) allows investors to cheaply and easily hold portfolios that more or less approximate the market portfolio. The enormous success of index funds and other instruments to achieve better and cheaper diversification is the practical counterpart to the triumph of the ideas of Modern Portfolio Theory, which showed that rational shareholders would want (under some assumptions, of course) to hold the market portfolio.16

However, Modern Portfolio Theory generally abstracts from the implications of portfolio diversification for competition. Firms are modeled as exogenous random endowments, or as price takers. For this reason, in the models used in Modern Portfolio Theory, the idea that common ownership could lead to monopoly is ruled out by assumption. This is not necessarily a criticism of Modern Portfolio Theory itself, since these are reasonable simplifying assumptions for the purposes for which the theory was developed, which is making good portfolio decisions. The point, however, is important to understand why there could be a major blind spot.

Around the same time that Modern Portfolio Theory was being developed, the modern theory of corporate governance emerged, centered on the problem of aligning managerial incentives with those of the firm’s shareholders.17 In economics, the object of study is too complex to develop models that are realistic along every dimension. For this reason, it is natural and understandable that both portfolio theory and corporate governance theory have generally abstracted from issues related to market power and competition.

I argue that this particular compartmentalization is problematic. The reason is that it is impossible to achieve the following objectives simultaneously: (i) portfolio diversification, (ii) shareholder representation, and (iii) competition. Portfolio diversification leads to all the companies having the same owners. In that case, if the companies act in the interest of their shareholders, the outcome of the economy is equivalent to that of a monopolist who owns all the firms. In Part III, I provide a formal statement and proof of this result (at a fairly abstract level), as well as several examples.

Part IV develops a theory of oligopolistic competition with overlapping ownership and managerial entrenchment. It shows that, while managerial entrenchment does mitigate the anticompetitive effects of common ownership, it does not eliminate them completely, except in the extreme case in which managers are so entrenched that they are ambivalent to shareholder dissent. Another result is that more concentrated owners within a firm have more control over it relative to management, and therefore lead to more internalization of common ownership incentives. This is in contrast to a model without managerial entrenchment, in which the effects of common ownership are the same whether it is generated by one thousand shareholders each holding 0.1 percent stakes, or by one large shareholder holding 100 percent in each firm. I provide some simple examples to illustrate these results.

I. Why Has Common Ownership Increased So Much?

A substantial body of empirical work has documented the ubiquity of common ownership among publicly traded firms, as well as its rapid rise in recent decades, using a variety of methodological approaches. For example, Professors Jarrad Harford, Dirk Jenter, and Kai Li showed that, for pairs of firms from the S&P 500 in 1985, the largest shareholder of one of the firms in the pair (the base firm) held on average 6.47 percent of that firm, and 0.45 percent in the other firm in the pair (the cross-held firm).18 Repeating the exercise in 2005 showed a large increase in common ownership, with the largest shareholder holding 8.98 percent in the base firm and 2.16 percent in the cross-held firm.19 My earlier work examining interlocking shareholdings of significant blocks showed that the density of the network of interlocking shareholdings among large US firms had more than doubled over the period 2000–2011.20 Work by Jan Fichtner, Eelke Heemskerk, and Javier Garcia-Bernardo showed that BlackRock, Vanguard, and State Street (the “Big Three” asset managers) were the largest shareholder in 88 percent of the S&P 500 firms in 2017.21

Attempting to provide a measure of common ownership that is more economically meaningful, my study with Professor Xavier Vives, as well as a study by Professors Matthew Backus, Christopher Conlon, and Michael Sinkinson, calculated the weight that large firms would place on their rival profits in their objective function, relative to their own profits, under a proportional control assumption (and assuming no agency frictions).22 Both studies show a large increase in this measure between the 1980s and the present. Common ownership is present not just in the United States but also to some extent in publicly traded European companies.23 The extent of common ownership in Europe seems to be less than it is in the United States, although more empirical work on European ownership patterns would be welcome.

Thus, the increase in common ownership is observed using a range of possible measures of shareholder overlap. There is somewhat less agreement on the causes of this increase. In earlier work, I argued that the rise of common ownership is a consequence of increasing portfolio diversification.24 The appearance of financial innovations such as index funds, index-tracking exchange-traded funds (ETFs), and quasi-indexer mutual funds have made portfolio diversification cheaper, more convenient, and more accessible to the general public over time.

The idea of holding a diversified portfolio in order to reduce risk is, of course, an old one. Modern Portfolio Theory refined this common-sense approach to investing and made it more precise. Theoretical work in the 1950s and early 1960s led to the development of the Sharpe-Lintner Capital Asset Pricing Model (CAPM).25 In the CAPM, every rational shareholder holds the market portfolio in equilibrium. At the same time, empirical work by Professor Eugene Fama and others supported the Efficient Markets Hypothesis, implying that prices quickly adjust to available information, and therefore future price changes are unpredictable.26 This combination of theory and empirics supported the view that even the best money managers could not beat the returns obtained by buying and holding a market portfolio.27

John Bogle recounted how this body of research inspired him to create the first index fund with his company, Vanguard:

[Professor Paul] Samuelson played a major role in precipitating the index fund’s creation. While I’d hinted at the idea of an index fund in my senior thesis at Princeton University in 1951 (mutual funds “may make no claim to superiority over the market averages”), Samuelson was much more forceful, strengthening my backbone for the hard task that lay ahead: taking on the industry establishment.

His article “Challenge to Judgment” caught me at the perfect moment. Published in the inaugural edition of the Journal of Portfolio Management in the autumn of 1974, it pleaded “that some large foundation set up an in-house portfolio that tracks the S&P 500 Index—if only for the purpose of setting up a naïve model against which their in-house gunslingers can measure their prowess.” . . . Vanguard Group (owned not by outsiders but by its own shareholders), I reasoned, ought to be “in the vanguard” of this new concept. Our goal was to offer well-diversified funds at minimal costs, focused on the long term. It was a marriage, as it were, made in heaven, strongly supported by the unequivocal data I assembled on fund performance and fund costs over the previous three decades.28

Despite initial skepticism from the financial industry, the index fund is today a resounding success and is still growing. Index funds comprise more than 80 percent of the equity assets of each of the Big Three asset managers.29

Of course, portfolio diversification could be achieved without index funds, and it would still lead to common ownership. However, in practice it is the rise of index funds that has led to overlapping holdings of large blocks of stock among almost all publicly traded firms. Low-cost index funds have fueled the growth of the Big Three, and this has led them to hold significant blocks in almost all companies. Figure 1 below shows how the fraction of firm pairs among the S&P 500 firms that have a common shareholder with at least a 5 percent blockholding in both firms has increased from almost zero in the 1980s to almost all firm pairs in 2017. Excluding the Big Three (plus Barclays Global Investors) from the calculation, however, leads to a much lower increase in interlocking shareholdings, with only about 5 percent of firm pairs having a common blockholder. The jump around 2010 is due to the acquisition of Barclays Global Investors by BlackRock during that period. This shows that the rise of common ownership of large blocks of stock is to a large extent a consequence of the rise of index funds and of the Big Three.

Figure 1: Percent of S&P 500 Firm Pairs That Have a Common Shareholder with at Least 5 Percent in Both Firms

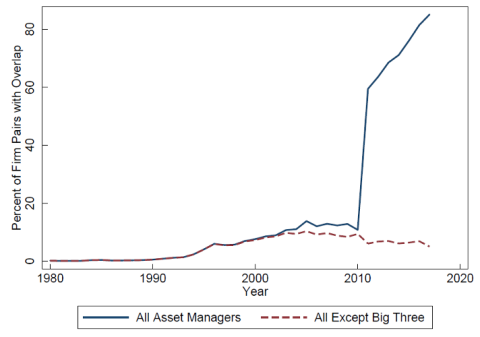
Thus, the rise of the index fund and of the Big Three has taken us from a “Berle-Means” world of dispersed ownership to a world of increasingly concentrated and overlapping ownership. According to Bogle, the transition to index funds leads to economies of scale that inherently lead to concentration and create barriers to entry for new potential competitors in the index fund market:

If historical trends continue, a handful of giant institutional investors will one day hold voting control of virtually every large US corporation. Public policy cannot ignore this growing dominance, and consider its impact on the financial markets, corporate governance, and regulation. These will be major issues in the coming era.

Three index fund managers dominate the field with a collective 81% share of index fund assets: Vanguard has a 51% share; BlackRock, 21%; and State Street Global, 9%. Such domination exists primarily because the indexing field attracts few new major entrants.

Why? Partly because of two high barriers to entry: the huge scale enjoyed by the big indexers would be difficult to replicate by new entrants; and index fund prices (their expense ratios, or fees) have been driven to commodity-like levels, even to zero. If Fidelity’s 2018 offering of two zero-cost index funds has established a new “price point” for index funds, the enthusiasm of additional firms to create new index funds will diminish even further. So we can’t rely on new competitors to reduce today’s concentration.30

The trend toward increasingly diversified portfolios is therefore largely due to the rational behavior of investors. The rise of index funds is simply a response to the demand for a cheap and convenient way to hold the market portfolio. And the rise of concentrated overlapping ownership is mostly due to the rise of the index funds, with the economies of scale in investing that inevitably go with that.

II. Firm Objectives Under Perfect and Imperfect Competition

This Part discusses the theory of the firm and shareholder representation under perfect and imperfect competition and frictions in shareholder representation introduced by managerial entrenchment and agency costs.

A. Firm Objectives Under Perfect Competition

Under perfect competition and complete markets, economic theory provides two arguments in favor of profit maximization as the objective of the firm: one based on shareholder welfare and the second based on broader social welfare. The first is based on the Fisher Separation Theorem literature,31 which shows that, if firms are price takers and markets are complete, all shareholders unanimously agree on the objective of profit maximization. The second is based on the First Welfare Theorem: if firms are price takers and markets are complete (and other assumptions are present, such as the lack of information asymmetries), then profit maximization by firms leads to a Pareto efficient outcome.

Professor Milton Friedman’s famous argument—that the only responsibility of business is to maximize profits—rests on the shoulders of these theoretical papers.32 His argument was twofold: First, managers should maximize profits because they are employed by their shareholders, and therefore they have a duty to them. A close reading shows that Friedman’s argument was that managers should maximize profits because that was what shareholders wanted:

In a free-enterprise, private-property system, a corporate executive is an employe[e] of the owners of the business. He has direct responsibility to his employers. That responsibility is to conduct the business in accordance with their desires, which generally will be to make as much money as possible while conforming to the basic rules of the society, both those embodied in law and those embodied in ethical custom.33

Therefore, Friedman was arguing for profit maximization as the objective of the firm as derived from a more basic principle, which is that firms should act in the interest of their shareholders. His argument implies that, if shareholders want something other than profit maximization, then managers should not maximize profits.

Friedman’s argument was essentially the same as the more recent argument by Professors Oliver Hart and Luigi Zingales that firms should not maximize shareholder value, but rather should maximize shareholder welfare.34 The only difference is that Friedman is focusing on the case when the Fisher Separation Theorem applies, so that shareholders unanimously agree on profit maximization.

Second, Friedman argues that maximizing profits is justified not only because of the duty of managers to their shareholders, but also because it leads to good outcomes for society as a whole. This, of course, echoes ideas encapsulated in the First Welfare Theorem.

B. Firm Objectives Under Imperfect Competition

The other side of the Fisher Separation Theorem coin is that, when firms are not price takers, there is no reason why shareholders should agree about the objective of profit maximization. The potential social responsibility of firms with market power was recognized by Friedman in Chapter 8 of his classic book Capitalism and Freedom:

Monopoly raises two classes of problems for a free society. First, the existence of monopoly means a limitation on voluntary exchange through a reduction in the alternatives available to individuals. Second, the existence of monopoly raises the issue of the “social responsibility,” as it has come to be called, of the monopolist. The participant in a competitive market has no appreciable power to alter terms of exchange; he is hardly visible as a separate entity; hence it is hard to argue that he has any “social responsibility” except that which is shared by all citizens to obey the law of the land and to live according to his lights. The monopolist is visible and has power. It is easy to argue that he should discharge his power not solely to further his own interests but to further socially desirable ends.35

In other words, with market power, the Fisher Separation Theorem does not apply, and shareholders may not agree on how to use that power. Prosocial shareholders may want to use that power in a way that does not lead to the highest possible level of profits, even in the long-term.

Similarly, the other side of the First Welfare Theorem is that, when firms are not price takers, maximizing profits does not lead to a Pareto efficient outcome. Therefore, monopoly is a market failure and it requires government intervention, either through antitrust enforcement or through regulation in the case of natural monopolies. For example, when firms generate externalities, stakeholder representation can lead to better social outcomes than pure shareholder representation.36

The failure of the Fisher Separation Theorem under imperfect competition creates a problem for the theory of oligopoly: What is the objective of firms when shareholders do not unanimously want profit maximization? Professor Kenneth Arrow’s impossibility theorem illustrates the complexity of the question.37 In a completely general way, it is not possible to derive an objective function for the firm from the individual objectives of the shareholders. Because of its enormous influence in the political economy literature, it is not widely known that Arrow was attempting to generalize the theory of the firm to cases with diverse shareholder objectives when he came up with the impossibility result:

When in 1946 I began a grandiose and abortive dissertation aimed at improving on John Hicks’s Value and Capital, one of the obvious needs for generalization was the theory of the firm. What if it had many owners, instead of the single owner postulated by Hicks? To be sure, it could be assumed that all were seeking to maximize profits; but suppose they had different expectations of the future? They would then have differing preferences over investment projects. I first supposed that they would decide, as the legal framework would imply, by majority voting. In economic analysis we usually have many (in fact, infinitely many) alternative possible plans, so that transitivity quickly became a significant question. It was immediately clear that majority voting did not necessarily lead to an ordering.38

While the problem of shareholder preference aggregation is quite challenging, it can be dealt with by relaxing the assumptions of Arrow’s impossibility theorem. Arrow was extremely ambitious in the required level of generality, since he wanted a way to obtain a social objective function from any possible set of individual preferences. He was also very ambitious in requiring that the preference aggregation be based purely on ordinal preferences—that is, ignoring any information on the intensity of preferences. We will need to relax the latter assumption in order to obtain a mapping from shareholder to firm objectives.

Professor Julio Rotemberg, as well as Daniel O’Brien and Professor Steven Salop, assumed that firms aggregate shareholder objectives through a weighted sum of their utilities.39 A natural generalization of this idea is that they maximize some function of shareholder utilities (which could be a weighted sum or a different function) where the function has as a parameter the ownership structure of the firm. I will use this idea in the next Part in which I formally state the trilemma. In Part IV, I generalize this in a different direction by considering a situation in which managerial objectives enter the objective of the firm, in addition to shareholder objectives.

The maximization of shareholder welfare advocated by Hart and Zingales40 is highly problematic from a social point of view, unless shareholders are altruistic. I argue that, if shareholders hold diversified portfolios (a possibility that Hart and Zingales abstract from since their model has only one firm41 ), then maximization of some shareholder welfare function leads to an economy-wide monopoly, as we will see in the next sections. This is the essence of the common ownership trilemma.

BlackRock CEO Larry Fink has called for companies to serve a social purpose and for companies to be run in ways that “benefit all of their stakeholders, including shareholders, employees, customers, and the communities in which they operate.”42

It is less clear which way the decisions would go when there is a trade-off among the different stakeholders in the long-term. For example, during a recent interview on CNBC’s “Squawk Box,” journalist Andrew Ross Sorkin asked Fink a question along these lines: “If all of these companies increase wages at the expense of their profits at least in the short term, how does a Black[R]ock think about that? It may be good for society but know it may be bad for the stock.”43

Fink answered along the lines of economic theories of efficiency wages—namely, that higher wages can help attract better workers, and make them more productive: “[I]f they believe they’re raising wages and are able to track better employees or the same employees but are now willing to work a little harder, they are more involved—if the output is better productivity, it may not deteriorate their margins.”44

This seems to be consistent with Professor Michael Jensen’s theory of enlightened value maximization, which is that, by paying attention to other stakeholders, firms may be able to attain the actual maximum value for shareholders.45 Of course, enlightened value maximization, in its essence, is simply a clarification of Friedman. Fink’s answer to Sorkin’s question is informative, and it also highlights how in many cases it may be difficult to separate governance activities involving social issues from questions of market power, such as the level of profit margins firms should aim for.

C. Managerial Entrenchment and Agency

Under both perfect and imperfect competition, the actual behavior of management will generally differ from what shareholders would want due to the existence of agency costs. Awareness of agency problems goes back at least to Adam Smith, who argued in The Wealth of Nations that the managers of publicly traded companies, because they were agents and not the direct owners of the company, would not take care of the business with the same level of attention as the partners in a privately held firm.46

More recently, Professors Bebchuk, Alma Cohen, and Hirst have argued that asset managers have incentives to underinvest in corporate governance.47 However, other studies show that the financial incentives for large asset managers to engage in corporate governance are substantial, due to their large size, and that the top asset managers have more incentives to be engaged in corporate governance than many activist funds: “[L]arge institutions like Black[R]ock gain substantially when firms in its portfolio do well, by virtue of the additional management fees they stand to receive if [assets under management] increases. Indeed, the largest institutional investors—because of their size—actually have stronger incentives to be engaged than many activist investors.”48

Field research based on more than fifty interviews of investors and companies by Patrick Jahnke also supports the view that large asset managers have strong incentives to engage in corporate governance: “For the largest index investors, the cost of engagement has fallen to a level where it is today negligible. The immense concentration amongst index funds, with the three largest fund managers controlling over 90 percent of assets, ensures sufficient return on their governance investments.”49

Bebchuk and Hirst argue that the corporate governance activities of large asset managers are unlikely to be effective.50 Their main argument is that they devote relatively limited resources to corporate governance, and in particular that they have a small number of people working in their governance teams, while they hold a large number of companies. For example, they argue that, because BlackRock had only 33 people in their stewardship team, while holding stakes in 17,309 companies, even if these employees focused only on companies in which BlackRock holds at least $1 billion in value, if they worked 250 days a year it would amount to only 3.17 person-days per company per year.51

There are, however, several reasons why their analysis is incomplete. First, the stewardship teams are growing (BlackRock’s stewardship team has grown to forty-three people according to the information on their website).52 Second, even though the corporate governance team is forty-three people, BlackRock is a large firm with more than ten thousand employees, and the corporate governance team can leverage research from their active portfolio managers, as well as external providers, as they explicitly indicate:

[W]e work closely with BlackRock’s active portfolio managers when engaging companies and in addressing relevant governance issues. Additionally, BlackRock’s investment teams leverage qualitative and quantitative company information, as well as sector and industry research, from various external service providers which can be used in [BlackRock Investment Stewardship’s] analysis of and conversations with companies and with clients.53

Third, and more importantly, in a steady state most companies may require minimal corporate governance engagement in order to protect long-term shareholder value. Only companies whose strategies and practices are inconsistent with long-term shareholder interests require engagement. Suppose that BlackRock focused on the largest two thousand companies around the world, which would account for the vast majority of its assets under management. Let’s assume that, on any given year, four out of five companies require minimal follow-up engagement, as their strategies are already aligned with long-term shareholder interests. This leaves substantial resources to engage with the remaining 20 percent of the firms that may require an adjustment in their long-term strategies. A team of 43 people, working 250 days a year, and 400 companies would imply about 27 person-days of full-time engagement per company, which is arguably enough to communicate the most important shareholder objectives to management.

While of course such a team would never be able to micromanage the operations of a firm, it could plausibly help steer the strategic plan of a company in the direction of joint profit maximization and help management avoid the temptation to deviate from a disciplined capital allocation industry equilibrium.

It is significant that corporate strategy and capital allocation plans are an explicit focus of engagement activities:

In order to make engagement with shareholders as productive as possible, companies must be able to describe their strategy for long-term growth. I want to reiterate our request, outlined in past letters, that you publicly articulate your company’s strategic framework for long-term value creation and explicitly affirm that it has been reviewed by your board of directors. This demonstrates to investors that your board is engaged with the strategic direction of the company. When we meet with directors, we also expect them to describe the Board process for overseeing your strategy.

The statement of long-term strategy is essential to understanding a company’s actions and policies, its preparation for potential challenges, and the context of its shorter-term decisions. Your company’s strategy must articulate a path to achieve financial performance.54

The empirical evidence is consistent with a mechanism operating at the broader strategic level, which requires only limited resources to communicate, rather than detailed micromanaging, which would require considerably more resources. For example, the effect of a carrier-level average common ownership across markets is an order of magnitude larger than the remaining effect of route-level common ownership.55 This suggests that common ownership affects the overall competitive strategic direction (for example, more aggressive or more disciplined capital allocation) of the firm much more effectively than product-specific behavior.

It is not implausible, therefore, that large asset managers have enough incentives and resources at their disposal to have a meaningful impact in the direction of companies to effectively protect and increase long-term shareholder value. This does not mean, of course, that shareholder value could not increase even more in a scenario in which even more resources were devoted to corporate governance. The agency problem is a real issue, and, as I will show, it implies that the more concentrated the ownership of companies, the higher the anticompetitive effects of common ownership.

III. The Trilemma

A. An Example

Consider a duopolistic industry in which two firms decide how much to invest in capacity. Each firm has two possible strategies: to invest aggressively in capacity, or to invest in a disciplined way. Suppose the firms are separately owned, each with ten shareholders, so shareholders of firm A care only about the profits of firm A, and the shareholders of firm B care only about the profits of firm B.

The payoff matrix for the shareholders in this game are the following:

		Firm B
		Aggressive	Disciplined
Firm A	Aggressive	(10, 10)	(20, 5)
	Disciplined	(5, 20)	(15, 15)

There is a unique Nash equilibrium of this game that involves both firms playing “Aggressive.” There is a prisoner’s dilemma situation in which both firms could be better off if they could coordinate to act in a disciplined way, but each has a unilateral incentive to deviate. In other words, in the absence of costly policing, collusive outcomes are not stable.

Suppose that instead of separate owners, the shareholders diversify their portfolios, so that each holds 5 percent of each firm. The payoff matrix for the shareholders now reflects the fact that each holds half of the portfolio in firm A and half in firm B:

		Firm B
		Aggressive	Disciplined
Firm A	Aggressive	(10, 10)	(12.5, 12.5)
	Disciplined	(12.5, 12.5)	(15, 15)

Note how the payoffs to each firm’s shareholders are the same for each pair of strategies. This is not a coincidence, but a natural consequence of portfolio diversification. Because of diversification, the firms have the same shareholders. Therefore, the utilities of the shareholders are the same. This changes the game quite a bit. In this case, the Nash equilibrium is both firms playing disciplined. This is the outcome that would occur if the two firms merged and acted as a monopolist. Note that, if the firm had some undiversified shareholders, they would be better off in the disciplined competition equilibrium than in the aggressive competition one, even though, as the first example illustrated, they individually would want the firm to deviate toward an aggressive strategy, so if they alone controlled the firm, capacity discipline would not be an equilibrium.

Even though in this extremely simple example the shareholders are unanimous within the firm, this is not essential to the monopoly equivalence result. To see this, consider a slightly more complicated example in which shareholders are not unanimous within the firm. Suppose that half of the (diversified) shareholders are also consumers of the product that the firms produce. Suppose that the higher prices in the outcome when both firms are disciplined create a loss (relative to the aggressive competition outcome) for the shareholder-consumers of 7, so their total utility is 8 in that case, and that they lose 4 in the case when only one firm is disciplined, so that their utility in that case is 8.5. This creates disagreement among the shareholders within each firm. The shareholders that are not consumers would like a fully disciplined approach. Those who are consumers, however, would want aggressive competition, because they would benefit from lower prices.

What would be the payoff matrix in this case? We need a way to combine the utilities of the different shareholders to obtain an overall payoff for the firm. Suppose that the firm weighs shareholders’ payoffs in proportion to their holdings (this is the objective function of the firm under proportional control according to O’Brien and Salop).56 In that case, the payoff for the firm when both firms are disciplined would be $(8 + 15) / 2$, that is, 11.5. The payoff when one firm is aggressive and one firm is disciplined would be $(8.5 + 12.5) / 2$, that is, 11:

		Firm B
		Aggressive	Disciplined
Firm A	Aggressive	(10, 10)	(11, 11)
	Disciplined	(11, 11)	(11.5, 11.5)

What would a monopolist do in this case? Suppose that the monopolist aggregates the utilities of the shareholders in proportion to their shares, as firm A and firm B would do. The monopolist chooses the capacity investment for both firm A and firm B. The payoff for the monopolist is 10 if both firms choose aggressive, 11.5 if they both choose disciplined, and 11 if one is aggressive and the other disciplined. Therefore, the monopolist would choose both firms’ strategies to be disciplined. We could change the parameters and come up with an example in which the monopolist would choose both firms’ strategies to be aggressive. In that case, the oligopoly Nash equilibrium with diversified portfolios would also result in aggressive behavior on the part of both firms.

B. More General Statement

This Section provides a formal statement and proof of the trilemma. The trilemma was stated previously within the context of a theory of oligopoly with shareholder voting.57 Here I provide a more general version, in which the objective function of the firm may or may not be obtained through a voting process. It is possible to write down voting models such that the objective function of the firm has the properties required for this proof, and voting models such that they don’t. I will go over examples of both these cases.

Consider an economy with a finite number J of firms. Firm j’s strategy is denoted $s_j$. The strategy could be unidimensional or multidimensional, in which case $s_j$ would be mathematically represented by a vector. There is a set I of shareholders that own the firms. Shareholder i owns a fraction $θ_{ij}$ of the shares in firm j. The utility of shareholder i is a function $u_i (s_1, . . .,s_J)$ of the strategies of the firms.

We assume that the objective function of firm j, which we denote as some function $F_j$ that aggregates the utilities of its shareholders. That is, firm j chooses $s_j$ to maximize $F_j(u_1, . . . ,u_I; θ_{1j}, . . ., θ_{Ij})$.

We can think of this function as summarizing the institutional and legal framework that determines control of a firm as a function of its ownership structure. The ownership shares are parameters of the function. As an example, in O’Brien and Salop under proportional control, the function $F_j$ would be the same for all firms and equal to $F(u_1, . . . ,u_I;θ_{1j}, . . .,θ_{Ij}=\sum_{i=1}^{I}θ+{ij}u_i$. Note that, although the aggregating function is the same, the objective function of the firms is not the same unless the firms have exactly the same shareholders. What is the same across firms is the way ownership translates into control.

We start by defining what we mean by oligopoly Nash equilibrium and by the monopoly outcome. We denote the utility-aggregating function of the monopolist $F_M$ and the ownership structure of the monopolist $(θ_{1M}, . . . θ_{IM})$ :

Definition 1 (Oligopoly Equilibrium). A Nash equilibrium of the oligopoly game is a set of strategies $(s_1*, . . . ,s_J*)$such that, for every firm j, $s_j*$ achieves the maximum of $F_j [u_1 (s_j ; s_{-j}*, . . .,u_I (s_j ; s_{-j}* ; θ_{1j}, . . . ,θ_{Ij} ]$ given the rival firm strategies $s_{-j}*$.

Definition 2 (Monopoly Outcome). A monopoly outcome is a set of strategies $(s_1^M, . . .,s_J^M)$ that achieves the maximum of $F_M[u_1(s_1, . . .,s_J, . . ., u_I(s_1, . . .,s_J);θ_{1M}, . . . θ_{IM}]$.

Assumption 1. All shareholders hold market portfolios in the oligopoly case. In the monopoly case, a shareholder’s share ownership of the monopolist is the same as her ownership of the market portfolio in the oligopoly case (formally, $θ_{ij} = θ_i$ for all j).

Assumption 2. There is a function $F(u_1, . . ., u_I ; θ_{1j} , . . ., θ_{Ij})$ that translates shareholder utilities into the objective of the firm, which is the same for all firms.

This assumption could apply if, for example, the institutional structure is such that managers are elected by majority voting. For example, Assumption 2 would be satisfied if the firm maximized the utility of the median voter (where the median is weighted by shares held in the firm). Under probabilistic voting, the firms will instead maximize a weighted average of shareholder utilities.58 As long as the distribution of the random component in the shareholder voting behavior varies only across shareholders and not across firms for a given shareholder, and there are no agency frictions, the function $F_j$ that summarizes how firms aggregate shareholder preferences will be the same across firms.

Other examples of shareholder preference aggregation functions that would satisfy Assumption 2 are the following: (i) maximization of a weighted average of shareholder utilities, when the weights are the Banzhaf voting power indices of the shareholders, (ii) maximization of the utility of the largest shareholder, (iii) maximization of a weighted geometric average of utilities, when the weights are proportional to shares, or to the Banzhaf indices.

The reason the probabilistic voting models in the literature tend to yield an objective function for the firm that is consistent with Assumption 2 is that there is no agency problem. Managers don’t have preferences for firm strategies, except due to the fact that they want to obtain shareholder support. Therefore, only shareholder preferences enter the objective function of the firm. Assumption 2, on the other hand, would not apply in models in which managerial utilities enter directly into the objective function of the firm. In the next Part, I develop an example in which managers are entrenched and have preferences over firm strategies directly and not only due to their need to obtain shareholder support. I will then show how Assumption 2 fails in that case. I will also make a technical assumption to ensure that the maximization problem of the monopolist has a unique solution.

Assumption 3. The objective function $F(u_1 , . . . , u_I ; θ_1, . . ., θ_I)$ is strictly quasi-concave (as a function of the strategies of the firms).

With these assumptions, we can show the following result:59

Proposition 1 (Common Ownership Trilemma). Under Assumptions 1–3, the oligopoly equilibrium and the monopoly outcome are unique, and they are equivalent.

Because it does not rely on a voting model, the proposition in this Essay is substantially more general than that in my earlier work. The outline of the proof, however, is similar. Intuitively, portfolio diversification implies that all the firms have the same shareholders, and so they all maximize the same objective function. It also happens to be the same objective function that a monopolist would maximize.

In the earlier literature, examples of cases in which portfolio diversification leads to a monopoly outcome consider cases in which shareholders are identical60 or make enough assumptions so that they are unanimous about joint profit maximization.61 It is therefore important to emphasize that this result actually has nothing to do with shareholder unanimity. More precisely, unanimity is neither necessary nor sufficient for the result.

To see why unanimity is not sufficient, consider, for example, the case of the Fisher Separation Theorem: shareholders are unanimous on the objective of profit maximization, and therefore the equilibrium is competitive, not monopolistic. Another reason why shareholder unanimity is not sufficient for a monopoly outcome is agency and managerial entrenchment, as we will see in Part IV. Suppose all shareholders hold market portfolios and are not consumers (nor workers, nor affected by externalities) so that they unanimously agree on joint profit maximization. If managerial objectives are firm-specific, and they influence the objective function of the firm, then the objective function of each firm is different, and the monopoly and oligopoly outcomes are different.

To see why unanimity is not necessary, consider the example previously discussed of heterogeneous shareholder consumers with market portfolios. Some shareholders consume more and some consume less relative to their ownership. They disagree on the objective of both the oligopolists and of the monopolists. The objective function of the oligopolistic firms is obtained through applying the aggregation function, and so is the objective function of the monopolist. Even though neither the shareholders of the monopolist nor of the oligopolists are unanimous, in both cases objective functions are the same, because they use the same F to aggregate shareholder utilities, and the ownership structure of both the monopolist and each of the oligopolists is identical, leading to the monopoly outcome being exactly the same as the oligopoly Nash equilibrium.

IV. Common Ownership and Competition with Managerial Entrenchment

The result from the previous Part provides a benchmark for what would happen if everyone held the market portfolio and shareholder representation was frictionless, which is that the equilibrium outcome under oligopolistic competition would be equivalent to the outcome under monopoly. What if we relaxed the assumption of frictionless shareholder representation? In this Part, we build a model of oligopolistic competition with common ownership and managerial entrenchment and show that the equivalence between oligopoly with market portfolios and monopoly breaks down, because the objective function of the firm is derived from both the objectives of the shareholders and of the management, which is firm-specific. In the context of homogeneous goods Cournot competition, we obtain a modified Herfindahl-Hirschman Index (MHHI), and show that the MHHI delta is lower when shareholders are less concentrated within a firm, as that exacerbates managerial entrenchment. This is consistent with the ideas expressed by Commissioner Phillips and others that agency costs mitigate the anticompetitive effects of common ownership.62

It is possible to write down a probabilistic shareholder voting model in which the equilibrium objective function of the firm is a weighted average of shareholder utilities, when the weights of the shareholders depend on their voting shares.63 In that model, managerial objectives do not enter the objective of the firm because the only objective of the managers is to obtain shareholder support. In practice, however, managers often have their own preferences over how the firm should be run. For example, managers may be empire builders when they obtain private benefits from running a larger firm. Alternatively, we could assume that managers may want to enjoy the quiet life and instead have preferences for a smaller firm that is easier to run, or that they want to maximize the profits of their own firm, perhaps because they directly own some shares.

Whatever managerial preferences over firm strategies are, if management is entrenched and faces no costs from shareholder dissatisfaction over the way the firm is run, the objective of the firm will be determined solely by the objective of the manager (which we can represent as an indirect utility function $u^M (s_1, ... ,s_J$ that the firm would maximize). This case of extreme managerial entrenchment is not realistic. Shareholder dissent is costly for management, even when they are entrenched. For example, there is empirical evidence that, even in uncontested elections, dissenting votes by shareholders have a negative impact on the careers of company board directors. In particular, one study found find that “increasing the votes withheld from the sample mean of 5.86% by 10% to 15.86% results in a 24% increase in the predicted director turnover probability.”64 The study also found that the effect is stronger at firms when firms do not have staggered boards.65 That is, dissenting shareholder votes hurt management less when the latter is entrenched.

Therefore, I consider instead a more realistic scenario, in which the incumbent management has preferences over strategies, but also faces a cost from shareholder dissent. In particular, I assume that the management faces a cost of being voted against in an uncontested election (even if the manager is not immediately replaced when enough votes are cast against). For simplicity, I assume that this cost is linear in the expected fraction of votes against received. The overall utility of the entrenched management is therefore:

$u^M (s_1, . . . ,s_J) = u_j^M (s_1, . . . ,s_J) - d \times (1- \sum_{i∈I} θ_{ij}ξ_i(s_1, . . . ,s_J))$ ,

where ξi denotes the probability that shareholder i votes in favor of the incumbent management. The parameter d captures how entrenched the incumbent management is, with d = 0 implying a fully entrenched management, and a d going to infinity implying a management that is not entrenched, because it faces a large cost of shareholder dissent.

In a model with two candidates, we assumed that shareholder i compared the utility it obtained as a result of each candidate’s strategy, and chose the candidate associated with the best strategy from this perspective. In the case of an incumbent manager, the shareholder must decide whether to vote for or against the management. I assume that there is a status quo strategy $s_j^{SQ}$ that represents the firm’s inherited strategy from the past. Shareholder i compares the utility it obtains from the incumbent management’s proposed strategy s and the utility it obtains from $s_j^{SQ}$ (conditional on the strategies it expects from the other firms $s_{-j}$), and it gives the manager a favorable vote only if the new strategy proposed by the management is better than the status quo strategy. However, as before, I assume that voting behavior is to some extent random from the point of view of the incumbent manager, and therefore add a random component to shareholder i’s decision. In particular, I assume that the probability that shareholder i votes in favor of the incumbent management is $G_i [u_i(s_j;s_{-j} - u_i(s_j^{SQ}s_{-j})]$ , where $G_i$ is the cumulative distribution function of a uniform with support $[-\frac{1}{2ψi}, \frac{1}{2ψi}]$. Throughout this Section, I will assume that $ψ_i=ψ$ for all i. This assumption is not crucial for our purposes but leads to cleaner and more easily interpretable expressions.

We say a strategy is a stable equilibrium for the firm if there is no incentive for the incumbent management to propose a different strategy and that strategy is the status quo. This equilibrium concept is often used from the political voting theory.66

Under these assumptions, a stable equilibrium strategy for the firm is the one that would maximize a weighted average of the utilities of the shareholders and of the entrenched management. The more entrenched the management is (that is, the lower is the cost d of shareholder dissent), the lower the weight that shareholder objectives receive relative to managerial objectives. Note that, if $u_M$ is constant, so that managers do not have their own preferences over firm strategies, and simply want to maximize shareholder support, the stable equilibrium in the model results in frictionless shareholder representation, and the firm maximizes a weighted average of shareholder utilities.

I apply this model of firm behavior to the Cournot competition context with shareholder-consumers and homogenous goods, and solve it under various alternative assumptions about managerial objectives. Shareholder i consumes $x_i(p)$ units of the monopolistic good when the price is p. The firms produce at constant marginal cost c and face an inverse demand curve p(q), some or all of which comes from shareholders themselves, where q is total quantity produced. I denote the absolute value of the elasticity of demand η. I assume throughout that shareholders do not perceive that their consumption decisions affect prices, which is reasonable given that the consumption decisions are made at the level of the individual shareholder and not the asset managers. Throughout this Section, $s_j$ refers to the market share of firm j.

As the baseline, I will assume that management would want to maximize the profits of the firm, perhaps because they own shares directly in the company. Formally, I assume that $u_M(p) = πj$ , that is, the agency problem is such that the incumbent managers want to maximize the profits of their firm, even when this is not the objective of their shareholders. I also assume that shareholders have quasi-linear utility $v(x_i) + y$ in the good that the firms produce and money.

In the case of monopoly, the objective of the firm is to maximize $π + \psi d \sum_{i \subseteq I} \theta_i [\theta_i π + v(x_i) - px_i ]$, which is equivalent to maximizing:

$π+\gamma\frac{\sum_{i \subseteq I} \theta_i [v(x_i) - px_i]}{\kappa}$

where $\gamma = \frac{\kappa \psi d}{1+ \kappa \psi d}$ and $\kappa$ is the within-firm ownership concentration HHI $\sum_{i \subseteq I} \theta_i^2$. With positive γ, shareholder objectives including consumption are taken into account. As γ goes to zero, agency frictions become so large that only managerial objectives are taken into account, and the firm becomes purely profit maximizing. As γ goes to one, agency frictions disappear, and only shareholder objectives determine the objective of the firm.

We can characterize the equilibrium markup as follows:

Proposition 2. The equilibrium markup in the monopoly model with $u_M = π$ is

$\frac{p-c}{p}=\frac{1-CIPI}{η}$, where $CIPI=μγ$

is the consumer internal power index, and $μ=(\sum_{iϵI}θ_i(x_i/q))/κ$, which measures the alignment between ownership of the monopolist and consumption.

As shareholder concentration within the firm κ increases, shareholder objectives have more weight. Also, as managers face higher costs of shareholder dissent, shareholder objectives have more weight. The same is true as shareholder voting becomes more deterministic (higher ψ). The agency problem reduces the consumer internal power index because managers only care about profits and therefore do not internalize the negative effects that higher prices generate for the owners of the firms in their role as consumers.

What is the equilibrium under oligopolistic competition with partial entrenchment, and does it converge to the monopolistic equilibrium? Analogously to the definition of stable equilibrium for the firm under monopoly with an incumbent manager, under oligopolistic competition we define a stable equilibrium for the industry as a set of strategies such that, if they are the status quo strategies of the firms, the Nash equilibrium strategies of the incumbent managers at every firm implies no deviation from the status quo.

Under oligopoly, the objective of firm j is to maximize $π_j+γ_j [\sum{k≠j}λ_{jk}π_k + \frac{\sum{iϵI}θ_{ij}[v(x_i)-px_i]}{\kappa_j}]$, where $\kappa_j = \sum{iϵI} θ_{i^2j}$ , $γ_j = \frac{\kappa_jψd}{1+ \kappa_jψd}$ , and $λ_{jk}=(1/κj)\sum_{iϵI} θ_{ij}θ+{ik}$ is the weight that firm j would put on firm k’s profits in the absence of agency frictions. I also define $μ_j = (\sum_{iϵI} θ_{ij} (x_i/q))/ \kappa_j$, which measures the alignment between ownership of firm j and consumption.

In this case, the markup is the following:

Proposition 3. The equilibrium markup in the oligopoly model with $u_j^M=π_j$ is $\frac{p-c}{p} = \frac{MHHI-CIPI}{η}$, where η is the elasticity of demand, $CIPI= \sum_{j=1}^{J}s_jμ_jγ_j$ is the consumer internal power index, and $MHHI = HHI + \sum{j=1}{J} \sum{k≠j}s_js_kλ_{jk}γ_j$ is the MMHI.

In this case, because of the factors $γ_j$, it is not true anymore that, when all shareholders hold the market portfolio, the MHHI is equal to one. The model of the oligopolistic equilibrium is also not equivalent to the monopolistic equilibrium, characterized in Proposition 2. The MHHI becomes the same as in the O’Brien and Salop model only in the limit, when all $γ_j$ go to one. Also, unlike the O’Brien and Salop model, the higher the concentration of ownership within a firm, the higher the MHHI delta. In a context of Bertrand competition, the model provides a microfoundation for the objective function in the structural model of Pauline Kennedy, O’Brien, Minjae Song, and Keith Waehrer (if $γ_j$ is the same across firms, it would be equivalent to their exogenous common ownership internalization parameter).67

These examples illustrate how introducing an agency problem through managerial entrenchment not only affects the equilibrium in both the monopoly and oligopoly models, but also breaks down the equivalence between the two when shareholders hold market portfolio. In the Appendix, I develop the cases in which managers are empire-builders or prefer a smaller firm (in other words, the quiet life). Although in those cases the markup is not proportional to an MHHI, it is still true that the equivalence between diversified portfolios oligopoly and monopoly breaks down.

To illustrate the model developed in this Section, I go through a numerical example of MHHIs with managerial entrenchment with more and less concentrated shareholders.

A. Managerial Entrenchment and the MHHI: Examples

Consider the following example: an oligopolistic industry with four symmetric firms (that is, each firm has a market share of 25 percent).68 The HHI is 2,500. Suppose the industry were owned by 1,000 small shareholders, each with 0.1 percent ownership in each of the four firms. In this case, the MHHI delta under the proportional control assumption would be 7,500. The MHHI would be 10,000—that is, equivalent to a monopoly in which just one shareholder held 100 percent of each of the four firms. This result is paradoxical, since it is counterintuitive that the 1,000 shareholders with 0.1 percent would be able to control the firms to the same extent as if there were just one concentrated shareholder of the whole industry, even if there is unanimity among the 1,000 small shareholders.

Consider now the MHHI delta in Professor Shapiro’s example, but adding entrenched management. Suppose, as an example, that the parameters ψ and d are such that ψ × d = 9. The ownership concentration HHI is, in the case of 1,000 small shareholders, equal to 0.001. Therefore, the MHHI delta is equal to 7,500 × 0.009 / 1.009, which is approximately 67. Therefore, the MHHI is 2,567, not much higher than the HHI. The anticompetitive effects from common ownership are low because the dispersion of the shareholders empowers management, and I have assumed that management maximizes the profits of the individual firm.

What if the four firms were held by just one large shareholder in this case? The ownership concentration HHI is equal to one in this case. Therefore, the MHHI delta is equal to 7,500 × 9 / 10, which is 6,750. The MHHI is 9,250, which is close to the monopoly level, implying that managerial entrenchment still mitigates the anticompetitive effects of common ownership, but much less, because the concentrated shareholder is able to influence management much more effectively.

Conclusion

I have argued that it is impossible to achieve simultaneously portfolio diversification, shareholder representation, and competition. This trilemma highlights the complexity of the policy analysis around common ownership, because the trade-off between diversification, shareholder representation, and competition requires making a decision on how to balance these mutually incompatible objectives.

If current trends continue, the competition issues associated with the rise of portfolio diversification are likely to grow. Professor John Coates has argued that the future of corporate governance will require us to address the “problem of twelve,” that is, that twelve individuals (representing institutions) will effectively control most publicly traded companies in the United States.69 Bogle warned that, if current trends continue, we are actually heading toward a problem of three:

Most observers expect that the share of corporate ownership by index funds will continue to grow over the next decade. It seems only a matter of time until index mutual funds cross the 50% mark. If that were to happen, the “Big Three” might own 30% or more of the U.S. stock market—effective control. I do not believe that such concentration would serve the national interest.70

Note that the reason that 30 percent of shares represent effective control is that less than 70 percent of shares are actually voted in director elections.71

American activist investor Bill Ackman has raised similar concerns. According to Ackman, in today’s environment, companies can “just dismiss the arguments that major shareholders make about their underperformance relative to competitors, about losing market share,” because “the index funds control America” and “are going to be the swing vote in every proxy contest in every election.”72

Ackman’s perspective is interesting because it highlights that activist investors today need to obtain approval of the large existing shareholders of a company, including the Big Three. Therefore, rather than mitigating the common ownership problem—as one would expect if they were fully taking over companies and turning them into more aggressive competitors—activists may exacerbate it by making managers less entrenched, while empowering their large shareholders.

The rise of common ownership is broad enough to potentially have macroeconomic consequences. In a simple macroeconomic model with common ownership, common ownership can have both anticompetitive and pro-competitive effects in general equilibrium.73 However, a calibration of the model showed that, if firms acted in the interests of their shareholders, the overall effect would be anticompetitive, and the rise of common ownership could help explain the pattern of secular stagnation observed over the past few decades, including increasing markups, the decline in the labor share, and the secular decline of equilibrium real interest rates.

Appendix

Proof of Proposition 1:

Under Assumptions 1 and 2, the objective function of every firm is the same: $F(u_1, . . . ,u_I;θ_1, . . . , θ_I)$. Since this function is strictly quasi-concave, it has a unique maximum as a function of the vector of firm strategies, which is the monopoly outcome $(s_1^M, . . . ,s_J^M)$. Strict quasi-concavity also implies that the monopoly outcome is a Nash equilibrium, and that there can be no other Nash equilibrium set of strategies, since it would have to be a local solution to the monopoly problem, but any local maximum would have to be a global maximum due to quasi-concavity.

Proof of Proposition 2:

The first-order condition is:

$p'q+p-c+(\frac{γ}{\kappa})\sum_{iϵI}θ_i(v'(x_i)∙x_i'p'-p'x_i-p∙x_i'p')=0$.

Roy’s identity implies that $v'(x_i)=p$, and therefore simplifies to:

$p-c=-p'(q-γ\frac{\sum_{iϵI}θ_ix_i}{\kappa})$.

Dividing by p, and then replacing $x_i = qµ_i$ and $-p'q/p=1/η$ yields the result in the proposition.

Proof of Proposition 3:

The first-order condition with respect to $q_j$ is (after applying Roy’s identity to simplify):

$p'q_j+p-c+p'γ_j[\sum_{k≠j}λ_{jk}q_k+\frac{\sum_{iϵI}θ_{ij}x_i}{\kappa_j}]=0$.

Solving for p-c and then dividing by p:

$\frac{p-c}{p}=-\frac{p'q}{p}\{q_j/q+γ_j[\sum_{k≠j}λ_{jk}q_k/q+\frac{\sum_{iϵI}θ_{ij}x_i/q}{\kappa_j}]\}$

$=\frac{s_j + γ_j\sum_{k≠j}λ_{jk}s_k-γ_jμ_j}{η}$ .

Taking a weighted average (with market shares as weights) on both sides of the equation yields the result in the proposition.

• 1See Erik P. Gilje, Todd A. Gormley, and Doron Levit, Who’s Paying Attention? Measuring Common Ownership and its Impact on Managerial Incentives *20–21 (working paper, Aug 24, 2018), archived at https://perma.cc/ZR79-C8FJ.
• 2Id at *22.
• 3See generally Daniel P. O’Brien and Steven C. Salop, Competitive Effects of Partial Ownership: Financial Interest and Corporate Control, 67 Antitrust L J 559 (2000). See also generally José Azar, A New Look at Oligopoly: Implicit Collusion Through Portfolio Diversification (unpublished PhD dissertation, Princeton University, 2012), archived at https://perma.cc/QH93-UU84.
• 4See José Azar, Martin C. Schmalz, and Isabel Tecu, Anticompetitive Effects of Common Ownership, 73 J Fin 1513, 1521–51 (2018); José Azar, Sahil Raina, and Martin Schmalz, Ultimate Ownership and Bank Competition *6–30 (University of Maryland Department of Economics Working Paper, Mar 17, 2016), archived at https://perma.cc/
  MW25-4HV4.
• 515 USC § 18.
• 6Einer Elhauge, Horizontal Shareholding, 129 Harv L Rev 1267, 1301–04 (2016).
• 7See id.
• 8Jonathan B. Baker, Overlapping Financial Investor Ownership, Market Power, and Antitrust Enforcement: My Qualified Agreement with Professor Elhauge, 129 Harv L Rev 212, 212 (2016).
• 9Eric A. Posner, Fiona M. Scott Morton, and E. Glen Weyl, A Proposal to Limit the Anticompetitive Power of Institutional Investors, 81 Antitrust L J 669, 708–09 (2017).
• 10Edward B. Rock and Daniel L. Rubinfeld, Antitrust for Institutional Investors, 82 Antitrust L J 221, 263–77 (2018).
• 11See id.
• 12Lucian A. Bebchuk and Scott Hirst, Index Funds and the Future of Corporate Governance: Theory, Evidence, and Policy, 119 Colum L Rev 2029, 2043–62 (2019).
• 13Noah Joshua Phillips, Taking Stock: Assessing Common Ownership, Remarks to the Global Antitrust Economic Conference at NYU Stern *10–11 (June 1, 2018), archived at https://perma.cc/H6FM-MRR5.
• 14Makan Delrahim, Don’t “Take the Money and Run”: Antitrust in the Financial Sector, Remarks to the Fordham University School of Law *3 (May 1, 2019), archived at https://perma.cc/LZJ2-WYC9.
• 15See Anna Tzanaki, The Regulation of Minority Shareholdings and Other Structural Links Between Competing Undertakings: A Law & Economics Analysis (unpublished PhD dissertation, University College London, 2017). See also Edward B. Rock and Daniel L. Rubinfeld, Common Ownership and Coordinated Effects *8–37 (NYU Law and Economics Research Paper No 18-40, Apr 1, 2019), archived at https://perma.cc/6U3V-4NPT.
• 16See generally Harry M. Markowitz, Portfolio Selection: Efficient Diversification of Investments (Yale 1959); William F. Sharpe, Capital Asset Prices: A Theory of Market Equilibrium Under Conditions of Risk, 19 J Fin 425 (1964); John Lintner, The Valuation of Risk Assets and the Selection of Risky Investments in Stock Portfolios and Capital Budgets, 47 Rev Econ & Stat 13 (1965).
• 17See, for example, Stephen Bainbridge, The New Corporate Governance in Theory and Practice 167–70 (Oxford 2008).
• 18Jarrad Harford, Dirk Jenter, and Kai Li, Institutional Cross-Holdings and Their Effect on Acquisition Decisions, 99 J Fin Econ 27, 38 (2011).
• 19See id.
• 20Azar, A New Look at Oligopoly at *51–54 (cited in note 3).
• 21Jan Fichtner, Eelke M. Heemskerk, and Javier Garcia-Bernardo, Hidden Power of the Big Three? Passive Index Funds, Re-Concentration of Corporate Ownership, and New Financial Risk, 19 Bus & Polit 298, 313 (2017).
• 22José Azar and Xavier Vives, Oligopoly, Macroeconomic Performance, and Competition Policy *6–13 (Centre for Economic Policy Research Discussion Paper No 13000, Dec 18, 2018), archived at https://perma.cc/7K5P-BSVP; Matthew Backus, Christopher Conlon, and Michael Sinkinson, Common Ownership in America: 1980–2017 *5 (National Bureau of Economic Research Working Paper No 25454, Jan 25, 2019), archived at https://perma.cc/B3C7-HHLV.
• 23See Paolo Siciliani and Daniel Norris, Bitesize: Common Ownership Across UK Banks: Implications for Competition and Financial Stability (Bank Underground, July 14, 2017), archived at https://perma.cc/KRP7-B3RM; José Azar and Martin C. Schmalz, Common Ownership of Competitors Raises Antitrust Concerns, 8 J Eur Competition L & Prac 329, 329, 331 (2017).
• 24Azar, A New Look at Oligopoly at *29 (cited in note 3).
• 25See generally Harry Markowitz, Portfolio Selection, 7 J Fin 77 (1952); Sharpe, 19 J Fin 425 (cited in note 16); Lintner, 47 Rev Econ & Stat 13 (cited in note 16).
• 26Eugene F. Fama, et al, The Adjustment of Stock Prices to New Information, 10 Intl Econ Rev 1, 7–17 (1969). See generally Paul A. Samuelson, Proof That Properly Discounted Present Values of Assets Vibrate Randomly, 4 Bell J Econ & Mgmt Sci 369 (1973).
• 27See generally Paul A. Samuelson, Challenge to Judgment, 1 J Portfolio Mgmt 17 (1974).
• 28John C. Bogle, How the Index Fund Was Born (Wall St J, Sept 3, 2011), online at https://www.wsj.com/articles/SB10001424053111904583204576544681577401622 (visited Oct 19, 2019) (Perma archive unavailable).
• 29Fichtner, Heemskerk, and Garcia-Bernardo, 19 Bus & Polit at 304 (cited in note 21).
• 30John C. Bogle, Bogle Sounds a Warning on Index Funds (Wall St J, Nov 29, 2018), online at https://www.wsj.com/articles/bogle-sounds-a-warning-on-index-funds-1543504551 (visited on Nov 2, 2019) (Perma archive unavailable).
• 31See, for example, Steinar Ekern and Robert Wilson, On the Theory of the Firm in an Economy with Incomplete Markets, 5 Bell J Econ & Mgmt Sci 171, 179 (1974); Roy Radner, A Note on Unanimity of Stockholders’ Preferences Among Alternative Production Plans: A Reformulation of the Ekern-Wilson Model, 5 Bell J Econ & Mgmt Sci 181, 181–84 (1974); S.J. Grossman and J.E. Stiglitz, On Value Maximization and Alternative Objectives of the Firm, 32 J Fin 389, 390 (1977); Harry DeAngelo, Competition and Unanimity, 71 Am Econ Rev 18, 26 (1981).
• 32See Milton Friedman, The Social Responsibility of Business Is to Increase its Profits, NY Times Mag 32, 33 (Sept 13, 1970).
• 33Id.
• 34Oliver Hart and Luigi Zingales, Companies Should Maximize Shareholder Welfare Not Market Value, 2 J L Fin & Acct 247, 270–71 (2017). See also Briefly 3.6: Who Do Corporations Serve? 9:15–14:35 (UCLR Online Podcast, Oct 16, 2019), online at https://lawreviewblog.uchicago.edu/2019/10/16/briefly-3-6-who-do-corporations-serve/ (visited Jan 15, 2019) (Perma archive unavailable) (discussing shareholder value and welfare with Professors Eric Posner and Luigi Zingales).
• 35Milton Friedman, Capitalism and Freedom 120 (Chicago 1962).
• 36See Michael Magill, Martine Quinzii, and Jean-Charles Rochet, A Critique of Shareholder Value Maximization *25–36 (Swiss Finance Institute Research Paper No 13-16, Mar 26, 2013), archived at https://perma.cc/3PSP-ZMN7.
• 37See generally Kenneth J. Arrow, A Difficulty in the Concept of Social Welfare, 58 J Polit Econ 328 (1950).
• 38Kenneth J. Arrow, Collected Papers of Kenneth J. Arrow: Social Choice and Justice 2 (Belknap 1983).
• 39Julio J. Rotemberg, Financial Transaction Costs and Industrial Performance *8 (Alfred P. Sloan School of Management Working Paper No 1554-84, Apr 1984); O’Brien and Salop, 67 Antitrust L J at 609–10 (cited in note 3).
• 40Hart and Zingales, 2 J L Fin & Acct at 248 (cited in note 34).
• 41Id at 252–55.
• 42Larry Fink, Larry Fink’s Annual Letter to CEOs: A Sense of Purpose (BlackRock, Jan 16, 2018), online at https://www.blackrock.com/hk/en/insights/larry-fink-ceo-letter (visited Oct 21, 2019) (Perma archive unavailable). A number of large companies recently issued a joint statement to similar effect. See David Gelles and David Yaffe-Bellany, Shareholder Value Is No Longer Everything, Top C.E.O.s Say (NY Times, Aug 19, 2019), online at http://www.nytimes.com/2019/08/19/business/business-roundtable-ceos-corporations.html (visited Oct 21, 2019) (Perma archive unavailable).
• 43CNBC Exclusive: CNBC Transcript: BlackRock Chairman and CEO Larry Fink on CNBC’s “Squawk Box” Today (CNBC, Apr 16, 2019), archived at https://perma.cc/VTR6-Z5SK.
• 44Id.
• 45Michael C. Jensen, Value Maximization, Stakeholder Theory, and the Corporate Objective Function, 12 Bus Ethics Q 235, 245–46 (2002).
• 46Adam Smith, An Inquiry into the Nature and Causes of the Wealth of Nations (Chicago 1976) (Edwin Cannan, ed) (originally published 1776).
• 47Lucian A. Bebchuk, Alma Cohen, and Scott Hirst, The Agency Problems of Institutional Investors, 31 J Econ Persp 89, 100–01 (2017); Bebchuk and Hirst, Index Funds at *29–31 (cited in note 12).
• 48Jonathan Lewellen and Katharina Lewellen, Institutional Investors and Corporate Governance: The Incentive to Be Engaged *17 (Tuck School of Business Working Paper No 3265761, Sept 1, 2018), archived at https://perma.cc/5J22-T9RL.
• 49Patrick Jahnke, Ownership Concentration and Institutional Investors’ Governance Through Voice and Exit, 21 Bus & Polit 327, 327 (2019).
• 50Bebchuk and Hirst, Index Funds at *32–36 (cited in note 12).
• 51Id.
• 52BlackRock Investment Stewardship: Protecting Our Clients’ Assets for the Long-Term *5 (BlackRock, Jan 2019), archived at https://perma.cc/CDM6-LLGX.
• 53Id at *9.
• 54Fink, Larry Fink’s Annual Letter to CEOs (cited in note 42).
• 55See generally Azar, Schmalz, and Tecu, 73 J Fin 1513 (cited in note 4).
• 56O’Brien and Salop, 67 Antitrust L J at 609–10 (cited in note 3).
• 57See Azar, A New Look at Oligopoly at *8 (cited in note 3).
• 58See id at *14–15; José Azar, Portfolio Diversification, Market Power, and the Theory of the Firm *12 (working paper, Aug 13, 2017), archived at https://perma.cc/3ZWK-ZTVW; Duarte Brito, et al, Unilateral Effects Screens for Partial Horizontal Acquisitions: The Generalized HHI and GUPPI, 59 Intl J Indust Org 127, 139 n 8 (2018).
• 59For proofs of the propositions, see Appendix.
• 60See Rotemberg, Financial Transaction Costs and Industrial Performance at *5 (cited in note 39).
• 61See Robert G. Hansen and John R. Lott Jr, Externalities and Corporate Objectives in a World with Diversified Shareholder/Consumers, 31 J Fin & Quant Analysis 43, 50 (1996).
• 62Phillips, Taking Stock at *10–11 (cited in note 13).
• 63See Azar, A New Look at Oligopoly at *16 (cited in note 3).
• 64Reena Aggarwal, Sandeep Dahiya, and Nagpurnanand R. Prabhala, The Power of Shareholder Votes: Evidence from Uncontested Director Elections, 133 J Fin Econ 134, 135–36 (2019).
• 65Id at 136.
• 66See Peter J. Coughlin, Probabilistic Voting Theory ch 6, 172–219 (Cambridge 1992).
• 67Pauline Kennedy, et al, The Competitive Effects of Common Ownership: Economic Foundations and Empirical Evidence *8 (Bates White Economic Consulting, July 26, 2017), archived at https://perma.cc/2228-MVGQ.
• 68I am grateful to Professor Carl Shapiro for suggesting this example at the 2015 FTC Microeconomics Conference.
• 69See generally John C. Coates, The Future of Corporate Governance Part I: The Problem of Twelve (Harvard Public Law Working Paper No 19-07, Sept 20, 2018), archived at https://perma.cc/S672-Z3H3.
• 70Bogle, Bogle Sounds a Warning (cited in note 30).
• 71See Bebchuk, Cohen, and Hirst, 31 J Econ Persp at 93 (cited in note 47).
• 72CNBC Exclusive: CNBC Transcript: Founder and CEO of Pershing Square Capital Management Bill Ackman Speaks with Scott Wapner Today (CNBC, Nov 6, 2017), archived at https://perma.cc/TB79-E6YS.
• 73See, for example, Azar and Vives, Oligopoly, Macroeconomic Performance, and Competition Policy at *4, 18–19 (cited in note 22); José Azar and Xavier Vives, Common Ownership and the Secular Stagnation Hypothesis, 109 AEA Papers & Proceedings 322, 325 (2019).