Causal AI—A VISOR for the Law of Torts

Causal AI is within reach. It has the potential to trigger nothing less than a conceptual revolution in the law. This Essay explains why and takes a cautious look into the crystal ball. Causation is an elusive concept in many disciplines—not only the law, but also science and statistics. Even the most up-to-date artificial intelligence systems do not “understand” causation, as they remain limited to the analysis of text and images. It is a long-standing statistical axiom that it is impossible to infer causation from the correlation of variables in datasets. This thwarts the extraction of causal relations from observational data. But important advances in computer science will enable us to distinguish between mere correlation and factual causation. At the same time, artificially intelligent systems are beginning to learn how to “think causally.”

I. Causation—Invisible to Humans and Machines Alike

Causation is the bedrock element of tort law. It is common to almost any cause of action. Without proof of causation, there is no tort and no liability. In the context of liability regimes based on fault, causation provides the necessary link between the two other elements necessary for a finding of responsibility: breach of duty by the defendant and damage to a protected interest of the plaintiff. For systems of strict liability that dispense with the fault or breach-of-duty requirement, the importance of causation is even greater. In the arena of no-fault liability, the finding of causation between the risk created and the damage done carries much of the burden of attribution.

As important as causation is in the law, it is anything but exclusive to the legal system. Rather, causation is a basic concept of human thought in general and of science in particular. Without a sound understanding of cause and effect, no car would move, no airplane would fly, no medication would be available, and no food could be prepared. It is no wonder, therefore, that the analysis of causation is a topic not only for lawyers, but also for scientists and philosophers. Where perspectives diverge and many different disciplines contribute, a stable consensus on what the concept actually means is difficult to attain. Causation is already a complex enough concept.

The rise of artificial intelligence poses additional challenges, primarily for artificial intelligence, not so much for conceptualizing causation. Causation is something of a threshold challenge for artificially intelligent computer systems. If a system can overcome this threshold, a whole new horizon of capabilities will open, and the law will be only one among a broad range of applications. Precisely because causation is such a fundamental concept in human thought, teaching computer programs how to identify causation would mean enormous progress. This is no mean feat, however. One of the pathbreaking philosophers thinking about causation is David Hume, and he famously believed that causation could not be observed in nature; it cannot be seen.1 All that can be observed is a series of events, one following the other. “We may define a cause to be ‘[a]n object precedent and contiguous to another, and where all the objects resembling the former are plac’d in like relations of precedency and contiguity to those objects, that resemble the latter’”; in other words where, if the first object had not been, the second never had existed.

The force or mechanism that causes a billiard ball to move when hit by a cue remains hidden. For this reason, an artificially intelligent computer system cannot learn to identify causation with the help of image recognition. There are just no images of causation to display. Large language models, which are in fashion at the time of writing, remain powerless in the face of causation as well. This is not to deny that such software systems are able to scan written material for text that talks about causation. If a large language model digested many texts that say that the ground gets wet when it rains, it will certainly be able to produce the correct answer when asked what happens to the ground when it rains. But this is not to say that the system understood anything about causation. Rather, everything depends on the texts used for training. At best, models of this type will be able to replicate knowledge about causation that we already have.

The question to investigate in this Essay moves beyond this naïve use of the concept of causation by artificially intelligent systems. The big question is whether a machine can be taught to think causally—to understand the meaning of the concept of causation. This requires that the meaning of causation can somehow be translated into computer code. It is imperative to program causal relationships in the sense that the computer system knows how to identify a situation of causal dependence (this is discussed in Part III). Before this possibility can be explored further, it is necessary to clear away some uncertainties and ambiguities that haunt the concept of causation in law as well as in economics (as discussed in Part II). As will hopefully become clear, the technological development has progressed to a point where “Causal AI” is within reach (see Part IV). If Causal AI works, it would equip the law of torts with something like a VISOR2 —a visual aid that enables decision-makers to “see” causation, if only in the digital world.

II. The Concept of Causation

The concepts of cause and causation are part of everyday language. People can talk about causation in a non-technical sense without thinking about the meaning of the term. Using the concept of causation in a colloquial sense captures the better part of its proper meaning.

1. Factual and Proximate Causation

In law, causation is a highly complex concept that comes in multiple layers. One fundamental distinction is between factual causation and proximate causation. While factual causation is about the factual relationship between the defendant’s conduct and the plaintiff’s harm, proximate causation determines whether the defendant is liable for all of the harm so caused or only for that fraction that is within the scope of the risk that was created by the defendant’s negligent or other conduct.

Proximate causation thus involves a normative, not a factual, analysis. This leads to the obvious conclusion that “[t]he so-called proximate cause issue is not about causation at all.”3 In the present context, it will be excluded from further analysis. The focus on factual causation alone raises questions that are complex enough, on which lawyers could certainly use some help from other sciences—and perhaps also from software tools that are artificially intelligent.

2. Forward-Looking (Predictive) and Backward-Looking (Evaluative) Causation

The concept of factual causation can be analyzed from multiple angles. The economic analysis of law has added a fundamental distinction, rarely discussed among lawyers: namely, the one between forward-looking and backward-looking causation.4 Forward-looking causation examines, ex ante, the probability that an act or event of a certain type will cause the type of harm in question. Backward-looking causation, in contrast, is not interested in the potential to cause harm measured in probabilities; rather, it asks whether, based on everything the court or other decision-maker knows about the situation ex post, an act or event actually caused the harm in question.

Legal systems understand the concept of causation to be backward looking, which leads to the application of the but-for test. Under the but-for test, any condition that was necessary for the harm to occur (i.e., absent which the harm would not have occurred in the situation at hand) is classified as a cause. While the but-for test has been analyzed and criticized for decades, it is remarkably persistent. By and large, the but-for test defines what legal systems believe factual causation is about.

3. Causation in Statistics and Computer Science

During the last thirty years, computer scientists have become increasingly interested in the concept of causation. For their own inquiry, they started from the same concepts and distinctions familiar from legal and economic analysis, distinguishing between general or type causation and specific or actual causation.5 This distinction maps onto the one between forward-looking and backward-looking causation set out above.6

The major advances in computer science regarding causation will primarily affect the category of forward-looking or type causation. Questions that are familiar from product liability, licensing of drugs and vaccines, responsibility for potentially toxic agents in water and foodstuffs, medical malpractice, and other areas come to mind. As can be gleaned from legal disputes in these areas, the question of causation is at once crucial to the outcome and impossible to settle with certainty. Often, the issue of causation remains open for years or decades until science has advanced to the degree that the harmful features of a substance or product can easily be established. The examples of cigarette smoke,7 asbestos products, and the drug DES8 are on point.

If it were possible to determine at a very early stage whether a particular product or substance was the cause of the harmful effects observed in the population, this would mean a huge advance for the well-being of individuals and society at large. If the risks associated with a product could be identified early on through a computer-driven analysis of the available data, much harm could be averted and much litigation avoided. All it takes to realize these benefits is a computer program that understands causation, in the sense that it can “see” causal relationships. In other words—causal AI.

III. From Correlation to Causation

Without much effort, researchers may identify a relationship of dependence, or correlation, between two variables within a dataset, as one variable changes its value together with changes in the value of the other.

1. Where We Come From: Correlation Does Not Imply Causation

With the birth of statistics as a discipline of the social sciences, the temptation arose to infer a type-level causal connection between two variables based on data that were collected or otherwise had become available. But to the present day, it is simply impossible to do so, at least on the basis of sets of observational data—data that were simply collected and not purposefully generated (for example, with the help of experiments). The analysis of observational data can only show a correlation between variables, but not a causal relationship. In this context, correlation means that the observation of event X changes the likelihood of observing event Y.9

Hume himself associated correlation with causation by employing the concept of regularity, as epitomized in his famous definition. Ordinary datasets reveal even less than Hume’s regularity condition, as correlation is non-directional; it is impossible to say whether Y follows X or X follows Y. So long as it remains impossible to infer causal relationships from the correlation between variables, the impact of statistics on causal reasoning remains limited, namely to the analysis of data drawn from experiments.

A few simple examples may help to illustrate the impossibility of inferring causation from correlation. If, on a weekday, the bells in the tower of Rockefeller Chapel strike five times to indicate that the time is 5pm, then there is always heavy traffic on Lake Shore Drive. But it is obvious to anyone that the striking of the church bells does not cause heavy traffic. The two events, the striking of the bells and the traffic jam, are merely correlated. Different, independent factors explain why the church bells strike and why the traffic is heavy.

Likewise, if ice cream sales increase with every additional degree of temperature, it is natural to infer that warm weather leads to additional consumption of ice cream.10 However, it can also be shown that when ice cream sales increase, crime rates go up. Again, it is intuitively clear that the sale of ice cream does not cause crime. The volume of ice cream sales and the crime rate are merely correlated, while there is a causal connection between warm weather and ice cream sales, and also between warm weather and the crime rate. Warm weather is a so-called confounder of the two independent phenomena. Together with hidden variables that are not included in the data (so-called colliders), confounders demonstrate why there is no bridge between correlation and causation.11

2. Within the Limitations of Experiments

Scientists who tried to establish a causal connection between a certain type of activity, agent, or event and another event (or, in the language of statistics, between X and Y) needed to resort to real-world experiments. The accepted mechanism for such a real-world experiment became the randomized controlled trial (RCT).12 RCTs are standard practice in many areas, including in the licensing of drugs. Before a drug is approved by the competent authorities, it must be shown that the drug has therapeutical effect—that it improves the patient’s health. This is done by forming two groups of patients, with all patients either having the same essential characteristics or being randomly chosen from the public, and then administering the drug to one group and a placebo to the other. If the treatment group fairs better than the control group, the therapeutic effect of the drug is established.

To this day, RCTs are the gold standard for establishing the causal connection between a condition and an effect, whether beneficial or detrimental. However, the method of random testing has serious limitations and disadvantages. To continue the example of a new medical treatment, drug testing comes with high costs and is contingent on preparatory trials and experiments—sometimes with animals—before humans may be exposed to substances with hitherto unknown consequences. Still, health risks remain. When the focus is not on substances designed to improve human health, but on ones that may have detrimental effects, ethical concerns loom large. It is unethical and not permissible to force a group of people to ingest substances that are presumed to be toxic or unhealthy (e.g., to smoke intensively or to consume large portions of processed food over years) in order to measure the adverse consequences that one fears would be caused by such consumption patterns.

The rise of computing and big data has further shifted the cost-benefit analysis. While the generation of experimental data through RCTs is terribly expensive and often even unfeasible, repositories of so-called observational data abound since the beginning of the digital revolution. The large internet companies, in particular, are in command of huge collections of observational data. Together with the computational power of up-to-date computers and the requisite software, these collections offer unique opportunities for statistical analysis. But as long as it remains impossible to read causation from observational data, these huge datasets are useless for causal analysis and thus for a better understanding of the world—as well as for the more expedient and precise, as well as less costly, operation of the legal system.

3. The Innovation: Causal Graphs and Models

Over the last few decades, scientists have engaged with the concept of causation and worked to wrench causal inference from observational data—in other words, to disentangle causation and “mere” statistical association.13 The goal is to reliably distinguish between instances where variables are merely correlated with no causal relation existing, and others where a causal connection and its direction can indeed be identified.

The traditional strategy used in statistics to distinguish causation from correlation without an RCT is controlling for variables that were suspicious to be confounders of the variables that represented cause and effect. If X and Y depend on a third factor, Z, that influences both, then the fact that X and Y move in parallel represents mere correlation—meaning X does not cause Y, but Z causes X and Y. It is possible to “control for” the fact that Z qualifies as a confounding variable, namely by conditioning on Z, which means that the researcher separates different values or strata of Z and then looks at the relationship between X and Y with respect to those values or strata. If, after controlling in this way for Z, X and Y still move in parallel, a causal relationship is established. Or so it seems.

One problem with conditioning on a variable is that it may make things worse by suggesting interdependence of two variables where none exists. This happens when researchers condition on so-called colliders: variables that, when held constant, create a spurious correlation between two variables that are, in fact, independent but contribute to the collider variable.14 The collider problem looms rather large because controlling for a variable that is both a confounder for some variables (e.g. X and Y) and a collider for other variables (e.g. A and B) solves one problem by creating another. Thus, the effort is set back to its starting point: mere correlation does not establish causation.

The “new statistics” setting in during the late 1990s and early 2000s aimed to move beyond the stage of controlling for variables. The new tools that promise to help draw the distinction between correlation and causation are Directed Acyclical Graphs (DAGs) and Structural Causal Models (SCMs). Such causal diagrams consist of a visualization of variables, together with arrows that link one variable to another. The arrows indicate the causal direction and are associated with mathematical equations which express the relationship between the two nodes connected by the arrow.

Figure 1: Casual Diagram for Birth Weight

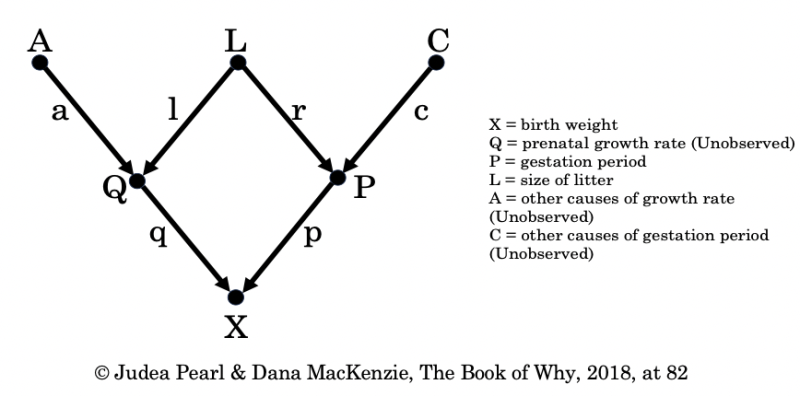
Once a causal model has been developed and applied to a set of observational data, it serves to illuminate the causal landscape in ways unknown before.15 One benefit is that causal models help to infer missing variables and causal connections by intervening in the model and changing one variable while holding the others constant. Moreover, the combination of a causal model and data enables researchers to quantify the effects of interventions without experiments.16 This means that it is possible to obtain the insights that would be generated by an RCT without actually performing one.17 In addition, the application of the model to observational data provides information on the adequacy of the model itself.

The question remains as to where DAGs and SCMs come from. They do not fall from the sky, and they cannot be found in “nature.” On the other hand, they are more than the pure product of the researcher’s imagination. Causal models and DAGs are based on the best scientific knowledge available, together with plausible beliefs about cause-and-effect relationships.

Causal diagrams cannot be drawn without knowledge about the world and the causal relations operating in it. Before drawing a DAG, the researcher must already know a lot not only about well-established causal relationships between the variables, but also about cause-and-effect relationships that are merely plausible.18 In doing so, they have no other choice but to rely on the best science, meaning whatever objective knowledge about cause and effect is already available, and their best guess based on their subjective view of the world and how it operates.19

In other words, causal models are products of the human mind, and therefore fallible. If a deficient causal model is applied to a clean dataset, it will produce conclusions that are wrong. Thus, for the foreseeable future human oversight and control still seem indispensable. As the outcomes reached by the combination of structural causal models and observational data crucially depend on the design and properties of the model chosen, choosing the right model is critical.

4. Digitalizing Causal Modelling

In view of the constant rise of computing power and AI software that is increasingly capable of developing and testing its own causal models, the automation of model generation itself has come within reach. The application of causal models to datasets itself provides a feedback loop that may be used as an internal control mechanism. As the model identifies dependencies and independencies between variables, it reveals information regarding the adequacy of the causal model itself.20 The same researchers who developed the field of causal inference in statistics have therefore also developed software tools that help to pick and choose the optimal causal model for a given research question given a dataset.

If this software worked perfectly, it would open the door to a fully automated analysis of causal relationships within a set of variables on which observational data are available. In this way, artificial intelligence would enable computers to autonomously identify causal relationships between variables in a set of observational data without any human involvement. Computers could infer causation from the combination of observational data and a self-selected causal model.

To pour some water into the wine, the capability of causal models to “test themselves” with the help of software or to allow researchers to test the model for its fitness may still be limited to so-called endogenous variables: variables that were included in the causal model. The choice of variables will usually reflect the data that are available; where data are missing, variables remain undefined. Undefined variables are treated as part of the (unchartered) “world” and lumped together in the variable U.21 As so-called exogenous variables, these U-variables are excluded from causal models and treated as given.

The problem is that within these hidden variables, a confounder may be buried that explains the dependence of Y on X. A hidden exogenous variable cannot be identified by controlling for an endogenous variable that sits in plain view. Thus, it seems that the accuracy of a causal model remains “internal,” in the sense that an accurate model is compatible with the dataset in question given the endogenous variables that the model contains.

Figure 2: Causal Inferences—Internal vs. External Variables

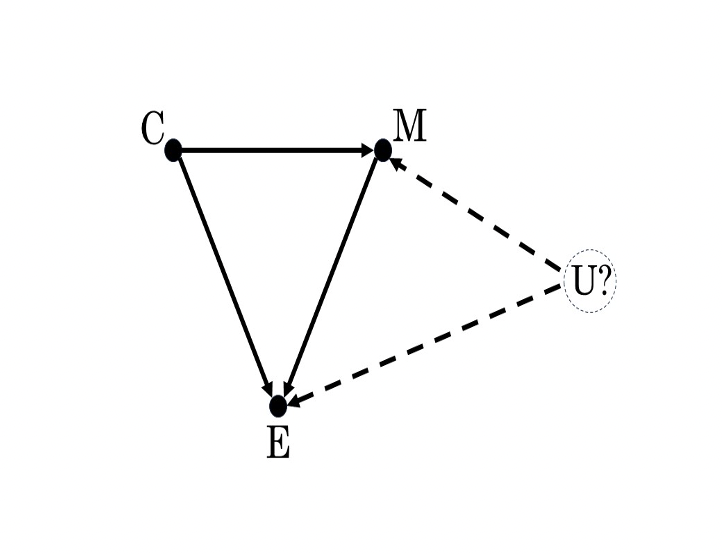
In the graph depicted above, the variable U is external to the causal model, which includes C, M, and E as internal variables (the dashed circle around U indicates as much). The dashed arrows from U to M and E suggest that U may have a causal effect on E as well as on M, and (indirectly) again on E. If so, these connections distort the causal inferences drawn from the graph, namely that C is a cause of E in two ways: direct and indirect, mediated through M.

The frontier problem in the field of causal inference concerns the exogenous variables and their bearing on the adequacy and completeness of causal models. If it were possible to rule out, with the help of computer-assisted mathematical analysis, that any variables that remained exogenous to the model influence the endogenous variables in a way that distorts the causal model, including its structural equations, then causal analysis could be formalized and computerized in full. Computers equipped with the necessary software could take over and extrapolate causal relationships from sets of observational data.

IV. Towards Casual AI

Once digital machines understand the concept of causation, one can speak of Causal AI. This will mark a major step in the development of digital systems truly deserving the label of artificial intelligence. With an understanding of causation, many errors and hallucinations that are characteristic of the current generation of large language models will disappear. With this, foundational models will advance to the next power level.

Causal AI will likely have a huge impact in different fields of science and learning. Once it is possible for a digital system to distinguish between correlation and causation in a pool of dependent variables, it can “see” causal relationships within a set of observational data. In the age of Big Data, such datasets are readily available at very low cost. It must therefore be expected that, with the arrival of Causal AI, knowledge about cause-effect relationships will increase dramatically in all areas, as if humanity were equipped with a visual aid that did not exist before.

From the perspective of the legal system, when assessing risk— either ex ante, for the purpose of regulating behavior or licensing drugs and other products, or ex post, in litigating liability for harm actually caused—Causal AI may play out its strengths and resolve uncertainties and controversies within a blink of an eye that hence have taken years or decades to resolve. To be sure, with all this good news, there may also be risks associated with the use of Causal AI—but their examination remains for another day.

* * *

Dr. Gerhard Wagner is the Chair of Civil Law, Commercial Law, and Economics at the Humboldt University of Berlin.

• 1See Stephen Mumford & Rani Lill Anjum, Causation 9–10 (2013).
• 2VISOR is a term from the Star Trek franchise, designating a visual aid that allows the blind to see. The acronym stands for Visual Instrument and Sensory Organ Replacement.
• 3Dan B. Dobbs, Paul T. Hayden & Ellen M. Bublick, Hornbook on Torts 338 (2d ed. 2016); see also David W. Robertson, The Common Sense of Cause in Fact, 75 Tex. L. Rev. 1765, 1766 (1997).
• 4See also William M. Landes & Richard A. Posner, The Economic Structure of Tort Law 229–34 (1987); Omri Ben-Shahar, Causation and Foreseeability, in Michael Faure, Tort Law and Economics 83, 85 (2009).
• 5Joseph Y. Halpern, Actual Causality 1 (2016).
• 6Id. at 2.
• 7For a discussion about developing a causal relationship between smoking and lung cancer, see Judea Pearl & Dana Mackenzie, The Book of Why 167–87 (2018).
• 8See generally Glen O. Robinson, Multiple Causation in Tort Law: Reflections on the DES Cases, 68 Va. L. Rev. 713 (1982).
• 9Pearl & Mackenzie, supra note 7, at 29.
• 10Judea Pearl, Madelyn Glymour & Nicholas P. Jewell, Causal Inference in Statistics 53 (2016). For similar examples, see Richard McElreath, Statistical Rethinking 123–44 (2d ed. 2020).
• 11Pearl & Mackenzie, supra note 7, at 219–34.
• 12Id. at 139–50.
• 13Pearl et al., supra note 10, at 53; McElreath, supra note 10, at 128–31.
• 14Pearl & Mackenzie, supra note 7, at 198–99.
• 15Pearl et al., supra note 10, at 35–36.
• 16Id. at 28, 56.
• 17See id. at 53; Pearl & Mackenzie, supra note 7, at 16–18.
• 18Judea Pearl, Causality 67 (2000).
• 19See Pearl & Mackenzie, supra note 7, at 89.
• 20Pearl et al., supra note 10, at 35, 48–50.
• 21Pearl et al., supra note 10, at 26–27. With a view to actual causation, see Halpern, supra note 5, at 13.